
11 SAT Math Formulas Every US Student Must Know
The SAT math test isn’t like any math test you’ve taken before. Its unique design, which challenges you to apply familiar concepts in unconventional ways, can be achieved with preparation. While it might be tricky, mastering the basic formulas and concepts covered on the test is your key to achieving a higher score.
What are these essential formulas, then? This comprehensive blog will discuss every critical formula you need to know before taking the SAT math section. Not only will it list them, but it will also break them down, ensuring you truly understand how they work. Grasping every formula on this list will save you precious time on test day and likely turn a few “maybe’s” into confident “yass” on your answer sheet.

Why Do the SAT Formulas Matter?
Formulas are like the building blocks of math. They give you a framework for understanding and solving problems. By knowing the key formulas, you’ll be able to approach any problem in the SAT math section with confidence.
However, not all formulas are created equal. When it comes to the SAT exam, there are a few key formulas that you absolutely need to know. These are the formulas that show up most frequently on the test and can be applied to a wide range of problems.
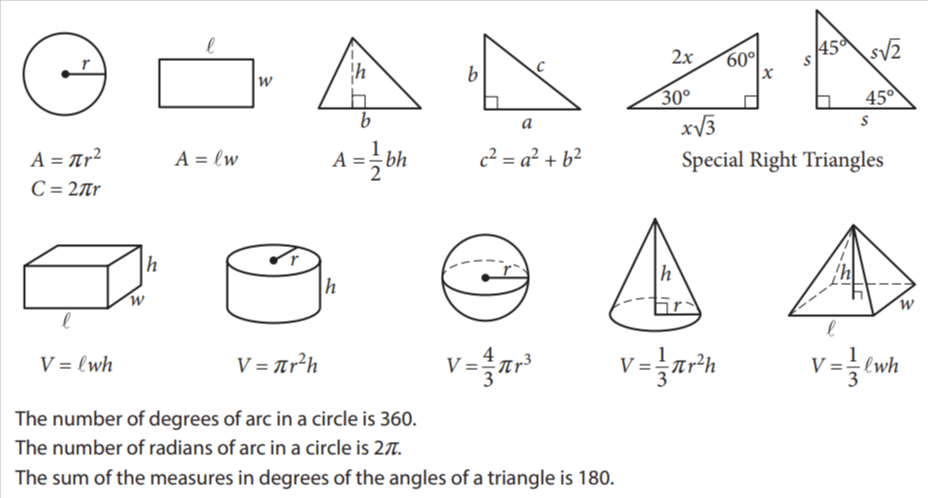
While only geometry formulas are provided in the actual SAT math section, memorizing them might seem helpful at first glance. However, it’s ultimately unnecessary and potentially time-consuming. Here’s why:
- Prioritize memorizing algebra and trigonometry: These make up a significantly larger portion (90% or more) of the test, and the provided reference sheet doesn’t include them.
- Limited usefulness: Geometry on the SAT typically accounts for only 10% of SAT math questions, so dedicating significant memorization effort to its formulas might not be the best use of your study time.
- Understand, not memorize: Knowing the underlying concepts behind the given geometry formulas is more valuable than rote memorization. The explanations provided will help you with that.
Must-Know SAT Math Formulas
Discover 11 essential SAT math formulas for exam success. Master these foundational tools to confidently tackle math problems on SAT test day.
Area of a circle and circumference of a circle
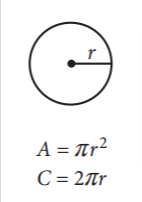
The area of a circle depends on its radius (r), which is the distance from the center of the circle to any point on its edge. Here’s how you can find the area of a circle:
A = πr²,
Where:
- A is the area of the circle.
- π (pi) is a mathematical constant approximately equal to 3.14159.
- r is the radius of the circle.
Circumference (C) = 2πr
The circumference of a circle is its perimeter, the total distance around its edge. We calculate it using pi (π) and the circle’s diameter, which is the distance straight across its center.
Area of a rectangle
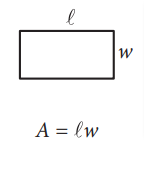
The area of a rectangle is the amount of space it encloses within its boundaries. The formula to calculate the area is simply the product of its length and width:
Area = Length x Width
Both length and width need to be measured in the same units for the calculation to be accurate. The final answer will also be in those units squared.
For example, if a rectangle has a length of 5 meters and a width of 2 meters, its area would be:
Area = 5 meters x 2 meters = 10 square meters
Area of a triangle
The area of a triangle with a base of length ‘b’ and a height of length ‘h’ is:
Area = (½) bh
- ½: This factor accounts for the fact that a triangle is half the size of a rectangle with the same base and height. Imagine cutting the triangle in half and rearranging the pieces side-by-side to form a rectangle.
- b: This represents the length of the base of the triangle. The base can be any side of the triangle as long as the height is measured perpendicular to it.
- h: This represents the length of the height of the triangle. The height is the segment perpendicular to the base drawn from a vertex of the triangle to the line containing the base.
This formula works for all types of triangles, regardless of their shape (scalene, isosceles, equilateral, etc.).
Pythagorean theorem
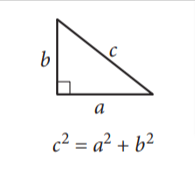
The Pythagorean Theorem is a fundamental relationship in Euclidean geometry that explains the connection between the sides of a right triangle. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs).
This can be expressed mathematically as:
c²+ a²= b²
where:
- c and a are the lengths of the two legs of the triangle
- b is the length of the hypotenuse
Special right triangle: isosceles triangle
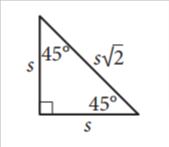
While an isosceles triangle has two equal sides and two equal angles opposite them, an isosceles right triangle takes it a step further: it always boasts a 90-degree angle flanked by two 45-degree angles.
s√2
This special relationship between its sides can be captured by the formula: √2 times the length of one side equals the hypotenuse (the side opposite the right angle).
In simpler terms, the hypotenuse is simply the length of a smaller side multiplied by √2. For example, an isosceles right triangle can have side lengths of 12, 12, and 12√2.
Special right triangle: 30, 60, 90-degree triangle
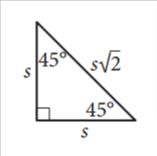
x√3
A 30-60-90 triangle, characterized by its interior angles of 30°, 60°, and 90°, exhibits a predictable relationship between its side lengths.
- The side opposite the 30° angle is the shortest, with a length equal to one unit.
- The side opposite the 60° angle, the middle length, is √3 times longer than the shortest side.
- Finally, the hypotenuse (opposite the 90° angle) is double the length of the shortest side or two units. This relationship can be seen in an example like a 30-60-90 triangle with side lengths of 5, 5√3, and 10.
Volume of a rectangular solid
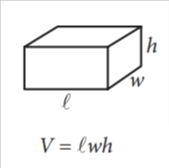
The volume of a rectangular solid is the amount of space it occupies. It’s calculated by multiplying the length, width, and height of the solid.
Here’s the formula:
Volume (V) = Length (l) × Width (w) × Height (h)
Where:
- V is the volume of the rectangular solid
- l is the length of the solid
- w is the width of the solid
- h is the height of the solid
To find the volume, simply measure the length, width, and height of the rectangular solid in the same units (e.g., centimeters, inches), then multiply the three values together.
For example, if a rectangular solid has a length of 5 cm, a width of 3 cm, and a height of 2 cm, its volume would be:
V = 5 cm × 3 cm × 2 cm = 30 cubic centimeters (cm³)
The units of volume will be the product of the units used for length, width, and height.
Volume of a cylinder
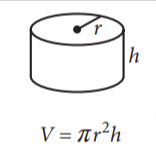
The volume of a cylinder is the amount of space it occupies, measured in cubic units. It can be calculated using the formula:
Volume (V) = πr²h
where:
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the cylinder’s base
- h is the height of the cylinder
Here’s how to understand the formula:
- πr² represents the area of the cylinder’s circular base.
- h represents the distance between the two circular bases.
Therefore, the volume is calculated by multiplying the area of the base by the height.
The units of radius and height should be the same (e.g., both in centimeters or meters) for the volume to be calculated correctly.
For example, if a cylinder has a base radius of 5 cm and a height of 10 cm, its volume would be:
V = π * 5² cm² * 10 cm
V = 78.54 cm³
Volume of a sphere
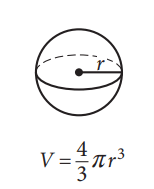
The volume of a sphere is the amount of space it occupies, measured in cubic units. It depends on the radius of the sphere, which is the distance from its center to any point on its surface.
The formula for the volume of a sphere is:
V = 4/3πr3
Where:
- V is the volume of the sphere
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the sphere
So, to calculate the volume of a sphere, you just need to know its radius and plug it into the formula.
Volume of a cone
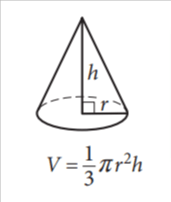
The volume of a cone is one-third the volume of a cylinder with the same base and height. We can use the formula for the volume of a cylinder to find the volume of the cone.
The volume of a cylinder is V = πr²h, where r is the radius of the base and h is the height of the cylinder.
The radius of the base of the cone is equal to the radius of the base of the cylinder, and the height of the cone is equal to the height of the cylinder. Therefore, the volume of the cone is:
V = ⅓πr²h
We can simplify this expression by combining the exponents:
V = ⅓πr²h
The volume of a cone is ⅓πr²h.
Volume of a pyramid
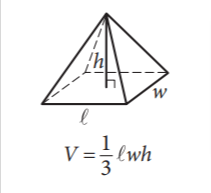
The volume of a pyramid is one-third the product of the area of the base and the height of the pyramid. In simpler terms, it’s the amount of space the pyramid occupies.
Here’s the formula to calculate the volume of a pyramid:
V = ⅓lwh
Where
- V is the volume of the pyramid
- w is the width of one of the edges of the rectangular part of the pyramid.
- h is the height of the pyramid
The base of a pyramid can be any shape, such as a triangle, square, rectangle, or pentagon. The height of a pyramid is the distance from the apex (the point at the top) to the base.
Suggested: 5 Best SAT Prep Books for 2024
From the Desk of Yocket
The SAT math formulas act as tools for solving a wide range of problems, from basic algebra to complex trigonometry. Having a solid grasp of these formulas can save you precious time and effort during the test, allowing you to focus on applying them strategically and creatively.
However, relying solely on rote memorization is not a clever move. The SAT isn’t just about memorizing formulas; it’s about understanding the underlying concepts and being able to apply them in the correct ways. Many students fall into the trap of memorizing formulas without truly comprehending their meaning, which can lead to confusion and frustration when faced with unfamiliar problems.
Instead of viewing formulas as magic spells, it’s more effective to think of them as guides to math problems. They offer a starting point, but the real challenge lies in understanding how to use them, where to use them, adapt to different problems, and reach the solution. Yocket is here to help you practice and master these techniques.
Frequently Asked Questions
What topics are covered in the SAT Math section?
The SAT Math section covers a wide range of topics, including
- Algebra: This includes topics such as linear equations, inequalities, functions, and graphs.
- Geometry: This includes topics such as lines, circles, triangles, and area and volume.
- Statistics and Probability: This includes topics such as data analysis, probability, and statistics.
Can I use a calculator for the SAT Math?
You can use a graphing calculator on 45 of the 58 math questions. The remaining 13 questions are designed to be solved without a calculator. The College Board provides a list of approved calculators on its website. Make sure your calculator is on the list before test day.
What is the format of the SAT Math section?
The SAT math section consists of 58 multiple-choice questions spanning three main areas: Heart of Algebra, Problem Solving and Data Analysis, and Passport to Advanced Math. You’ll have 80 minutes to complete the section. Some questions allow the use of a graphing calculator, while others don’t.
