11 Hardest SAT Math Questions With Answer in 2024

Ever felt like the SAT Math section was speaking a whole different language? You’re not alone. Many students find themselves struggling with these challenging questions, which can make it tough to get a good score on the SAT exam.

The SAT Math section is known for its challenging questions, often leaving students scratching their heads and wondering where they went wrong. But fear, not because we’re here to simplify the SAT Math and guide you through some of the most perplexing questions it throws your way.

In this blog post, we’ll tackle 11 of the most difficult SAT Math questions, providing step-by-step solutions and breaking down each concept in a way that most students can understand. So, whether you’re aiming for a perfect score or just trying to survive the SAT Math section, this guide is for you.

SAT Math Section: A Brief Overview

Before we begin with the most difficult questions, let’s take a quick look at the SAT Math section.

The Math Test is divided into two parts: no calculator and calculator. For the no-calculator portion, you’ve got 25 minutes to tackle 20 questions. That gives you about 1 minute and 15 seconds per question. On the calculator portion, you’ll have 55 minutes to handle 38 questions, which means you’ll have about 1 minute and 26 seconds per question.

Don’t worry about not having a calculator for one section of the SAT Math. The questions in this section are more about understanding concepts than doing complicated calculations.

The calculator section is usually tougher than the no-calculator section. Without a calculator, it’s all about how quickly and accurately you can solve problems.

Questions on the SAT Math Test are distributed among these three topics:

• 19 Heart of Algebra questions
• 17 Problem Solving and Data Analysis questions
• 16 Passport to Advanced Math questions

The remaining six questions test your understanding of additional topics in math such as area, volume, circles, triangles, and trigonometry.

Be sure to practice using the facts and SAT math formulas below. The more you practice, the better you’ll be at using them accurately and quickly.

Source: College Board

The Math Test is mostly multiple-choice, with about 80% of the questions being this type. The other 20% of the questions are gridded-response, which means you’ll need to write in your answer instead of choosing from a list of options. For these questions, you’ll need to enter your answer (a number, fraction, or integer) into a grid on the answer sheet.

If you’re stuck on a question, don’t waste time on it. Just skip it for now and come back to it later. Make sure to mark it in your booklet so you don’t forget.

Suggested: When to Take the SAT Exam

11 SAT Hard Math Questions Solved

Typically, these official hardest SAT math questions are arranged from easy to hard, with the simpler ones presented first and the more challenging ones placed towards the end. This pattern holds true for both multiple-choice and student-written questions, so anticipate that the later questions, especially the harder SAT math questions, may take longer to tackle than the earlier ones.

Discover the 11 hardest SAT math questions ever with detailed answers and practice to enhance your skills.

Remember to tackle the easier questions first, so you have more time for the tougher ones.

Question 1: Line ℓ is graphed in the xy-plane below.

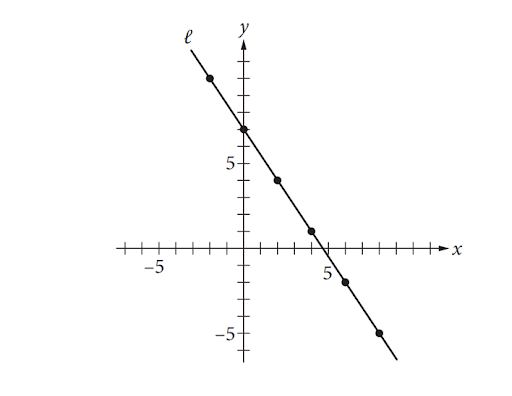
If line ℓ is translated up 5 units and right 7 units, then what is the slope of the new line?

1. 25
2. −32
3. −89
4. −1114

Answer: B

Explanation: Choice B is correct. The slope of a line can be determined by finding the difference in the y-coordinates divided by the difference in the x-coordinates for any two points on the line. Using the points indicated, the slope of line ℓ is −32. Translating line ℓ moves all the points on the line to the same distance in the same direction, and the image will be a line parallel to ℓ. Therefore, the slope of the image is also −32.

Question 2: The average number of students per classroom, y, at Central High School can be estimated using the equation y = 0.8636x + 27.227, where x represents the number of years since 2004 and x ≤ 10. Which of the following statements is the best interpretation of the number 0.8636 in the context of this problem?

1. The estimated average number of students per classroom in 2004
2. The estimated average number of students per classroom in 2014
3. The estimated yearly decrease in the average number of students per classroom
4. The estimated yearly increase in the average number of students per classroom

Answer: D

Explanation: Choice D is correct. When an equation is written in the form y = mx + b, the coefficient of the x-term (in this case, 0.8636) is the slope of the graph of this equation in the xy-plane. The slope of the graph of this linear equation gives the amount that the average number of students per classroom (represented by y) changes per year (represented by x). The slope is positive, indicating an increase in the average number of students per classroom each year.

Since there’s no penalty for guessing answers on the SAT, don’t leave any questions blank! For tricky ones, try to eliminate some answer choices before making your pick.

Question 3: If 2a − 1 = 4y, y ≠ 0 where a ≠ 1, what is y in terms of a?

1. y = 2a − 2
2. y = 2a − 4
3. y = 2a − 1a
4. y = yaa + 1

Answer: A

Explanation: Choice A is correct. Multiplying both sides of the equation by the denominators of the rational expressions in the equation gives 2y = 4a − 4. You should then divide both sides by 2 to isolate the y variable, yielding the equation y = 2a − 2.

Question 4: The recommended daily calcium intake for a 20-year-old person is 1,000 milligrams (mg). One cup of milk contains 299 mg of calcium, and one cup of juice contains 261 mg of calcium. Which of the following inequalities represents the possible number of cups of milk, m, and cups of juice, j, a 20-year-old person could drink in a day to meet or exceed the recommended daily calcium intake from these drinks alone?

1.  299m + 261j ≥ 1,000
2.  299m + 261j > 1,000
3. 299m + 261j ≥ 1,000
4. 299m + 261j > 1,000

Answer: A

Explanation: Choice A is correct. Multiplying the number of cups of milk by the amount of calcium each cup contains and multiplying the number of cups of juice by the amount of calcium each cup contains gives the total amount of calcium from each source. You must then find the sum of these two numbers to find the total amount of calcium. Because the question asks for the calcium from these two sources to meet or exceed the recommended daily intake, the sum of these two products must be greater than or equal to 1,000.

Don’t get stuck on any one question for too long. You’ll have about a minute and fifteen seconds for each question without a calculator and a bit less than a minute and a half for questions with a calculator.

Question 5: A research assistant selected 75 undergraduate students at random from the list of all students enrolled in the psychology degree program at a large university. She asked each of the 75 students, “How many minutes per day do you typically spend reading?” The mean reading time in the sample was 89 minutes, and the margin of error for this estimate was 4.28 minutes. Another research assistant intends to replicate the survey and will attempt to get a smaller margin of error. Which of the following samples will most likely result in a smaller margin of error for the estimated mean time students in the psychology degree program read per day?

1. 40 undergraduate psychology-degree program students selected at random
2. 40 undergraduate students selected at random from all degree programs at the university
3. 300 undergraduate psychology-degree program students selected at random
4. 300 undergraduate students selected at random from all degree programs at the university

Answer: C

Explanation: Choice C is correct. Increasing the sample size while randomly selecting participants from the original population of interest will most likely result in a decrease in the margin of error.

Question 6: A company’s manager estimated that the cost C, in dollars, of producing n items is C = 7n + 350. The company sells each item for $12. The company makes a profit when the total income from selling a quantity of items is greater than the total cost of producing that quantity of items. Which of the following inequalities gives all possible values of n for which the manager estimates that the company will make a profit?

Remember to solve an inequality just as you would an equation, with one important exception. When multiplying or dividing both sides of an inequality by a negative number, you must reverse the direction of the inequality: If −2x > 6, then x < −3.

1. n < 70
2. n < 84
3. n > 70
4. n > 84

Answer: C

Explanation: Choice C is correct. One way to find the correct answer is to create an inequality. The income from sales of n items is 12n. For the company to profit, 12n must be greater than the cost of producing n items; therefore, the inequality 12n > 7n + 350 can be used to model the context. Solving this inequality yields n > 70.

Question 7: At a primate reserve, the mean age of all the male primates is 15 years, and the mean age of all female primates is 19 years. Which of the following must be true about the mean age m of the combined group of male and female primates at the primate reserve?

1.  m = 17
2. m > 17
3. m < 17
4. 15 < m < 19

Answer: D

Explanation: Choice D is correct. You must reason that because the mean of the males is lower than that of the females, the combined mean cannot be greater than or equal to that of the females, while also reasoning that because the mean of the females is greater than that of the males, the combined mean cannot be less than or equal to the mean of the males. Therefore, the combined mean must be between the two separate means.

Question 8: A researcher wanted to know if there is an association between exercise and sleep for the population of 16-year-olds in the United States. She obtained survey responses from a random sample of 2,000 United States 16-year-olds and found convincing evidence of a positive association between exercise and sleep. Which of the following conclusions is well supported by the data?

1. There is a positive association between exercise and sleep for 16-year-olds in the United States.
2. There is a positive association between exercise and sleep for 16-year-olds around the world.
3. Using exercise and sleep as defined by the study, an increase in sleep is caused by an increase in exercise for 16-year-olds in the United States.
4. Using exercise and sleep as defined by the study, an increase in sleep is caused by an increase in exercise for 16-year-olds in the world.

Answer: A

Explanation: Choice A is correct. A relationship in the data can only be generalized to the population that the sample was drawn from.

Question 9: A biology class at Central High School predicted that a local population of animals would double in size every 12 years. The population at the beginning of 2014 was estimated to be 50 animals. If P represents the population n years after 2014, then which of the following equations represents the class’s model of the population over time?

1. P = 12 + 50n
2. P = 50 + 12n
3. P = 50(2)12n
4. P = 50(2)n12

Answer: D

Explanation: Choice D is correct. A population that doubles in size over equal time periods is increasing at an exponential rate. In a doubling scenario, an exponential growth model can be written in the form y = a(2)nb, where a is the initial population (that is, the population when n = 0) and b is the number of years it takes for the population to double in size. In this case, the initial population is 50, the number of animals at the beginning of 2014. Therefore, a = 50. The text explains that the population will double in size every 12 years. Therefore, b = 12.

Question 10: The function f is defined by f(x) = 2x3 + 3x2 + cx + 8, where c is a constant. In the xy-plane, the graph of f intersects the x-axis at the three points (−4, 0), (12, 0), and (p, 0). What is the value of c?

1. −18
2. −2
3. 2
4. 10

Answer: A

Explanation: Choice A is correct. The given zeros can be used to set up an equation to solve for c. Substituting −4 for x and 0 for y yields −4c = 72, or c = −18. Alternatively, since −4, 12, and p are zeros of the polynomial function, it follows that f(x) = (2x − 1)(x + 4)(x − p). Were this polynomial multiplied out, the constant term would be (−1)(4)(−p) = 4p. (We can grasp this without performing the full expansion.) Since it is given that this value is 8, it follows that 4p = 8, or, rather, p = 2. Substituting 2 for p in the polynomial function yields f(x) = (2x − 1)(x + 4)(x − 2), and after multiplying the factors, one finds that the coefficient of the x term, or the value of c, is −18.

Question 11: The equation c = 59 (f – 32) shows how temperature f, measured in degrees Fahrenheit, relates to temperature c, measured in degrees Celsius. Based on the equation, which of the following must be true?

1. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius.
2. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
3. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

1. 1 only
2. 2 only
3. 3 only
4. 1 and 2 only

Answer: D

Explanation: Choice D is correct. Consider the equation as an equation for a line y = mx + b, where c = 59 (f – 32) or c = 59f − 59 (32). As you can see, the slope of the graph is 59, which means that for an increase of 1 degree Fahrenheit, the increase is 59 of 1 degree Celsius. c  = 59 (f) and c = 59(1) = 59. Hence, statement 1 is true. This is equivalent to saying that an increase of 1 degree Celsius is equal to an increase of 59 degrees Fahrenheit. 

c = 59(f)

1 = 59 (f)

(f) = 59

Since 59 = 1.8, statement 2 is true.

Note: All of the SAT Math Test questions are based on the College Board’s official study guide.

Read also: Top 125 SAT Vocabulary Words for 2024

From the Desk of Yocket

In the SAT Math Test, you’ll be presented with multi-step problems that draw on concepts from science, social science, careers, and other everyday situations. Some problems will even give you a scenario and ask you multiple questions related to it.

The SAT Math Test wants to see if you really understand math, not just how to do the math. It wants to know if you can use math to solve problems, no matter what the problem is. So, you’ll need to have both a deep understanding of mathematical concepts and the ability to apply those concepts to real-world situations. It’s not just about memorizing formulas and procedures. It’s about being able to think like a mathematician and apply math to the world around you.

Conceptual understanding and procedural skill fluency go hand in hand. Together, they lead to a thorough understanding of mathematical ideas and methods for solving problems. Questions on the SAT Math Test assess these skills in various ways because the ability to use mathematical ideas and methods flexibly shows an understanding of math that can be applied to a wide variety of settings.

The more you understand math, the better you’ll be at using it to solve problems. And the more you practice using math, the better you’ll become at understanding it. So don’t just focus on memorizing formulas or tricks. Make sure you’re also taking the time to understand the “why” behind the math. For additional help, connect with our Yocket team, who can provide valuable insights and guidance to enhance your skills.

---

Frequently Asked Questions

1. How is the SAT Math section scored?

The SAT Math section is scored on a scale of 200 to 800. Your score will be based on the number of questions you answer correctly. There is no penalty for guessing in the SAT Math section.

2. What is a good SAT Math score?

A score of 500 is considered average, while a score of 600 is considered good. A score of 700 or higher is considered excellent.

3. What is the highest and lowest possible SAT Math score?

The highest possible SAT Math score is 800, and the lowest possible SAT Math score is 200.