20 Critical ACT Math Formulas You Must Know

Feeling anxious about the ACT Math section because there’s no formula sheet? Relax! This blog is your guide to mastering ACT Math, even without formulas by your side. We’ll equip you with the must-know formulas you need to ace the test with confidence. We’ll break down these essential formulas into clear, understandable categories. No more panicking during the test; you’ll have a structured understanding of the formulas you need to apply, making them effortless to recall and use. Yocket is here to support your preparation journey, ensuring you approach the ACT Math section with confidence and success.

20 ACT Math Formulas

Discover 20 ACT math formulas every US student should know.

1. Rectangle: Area = Length x Width

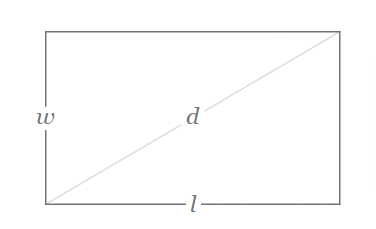
The formula accurately represents the relationship between the dimensions and the area of a rectangle. So, the formula essentially states that the area of a rectangle is calculated by multiplying its length and its width.

2. Triangle: Area = ½ Base x Height

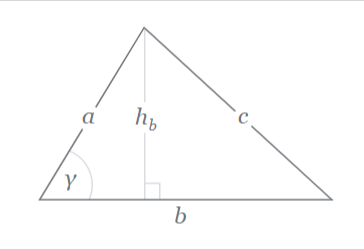
The area of a triangle can be calculated using the formula 1/2 Base x Height, where base refers to any side of the triangle and height is the perpendicular distance from that base to the opposite vertex. This formula holds true for all types of triangles, whether they are right-angled, isosceles, scalene, or equilateral.

3. Circle: Area = πr² Circumference = 2πr (π ≈ 3.14)

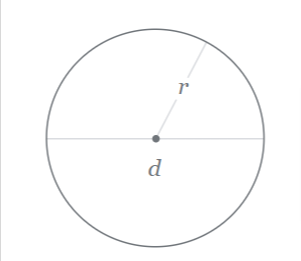
This formula explains the relationship between two key properties of a circle: its area and its circumference. The area of the circle is calculated by multiplying π by the radius squared.

4. Cylinder: Volume = πr²h

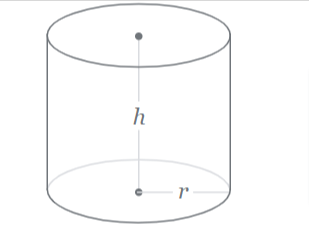
The formula Volume = πr²h tells you that the volume of a cylinder is found by multiplying the area of its base (πr²) by its height (h).

5. Sphere: Volume = (43)πr³

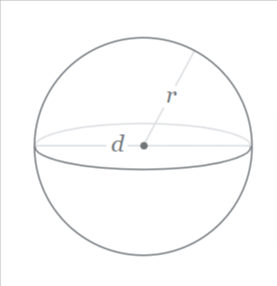
This formula essentially tells you that the volume of a sphere is proportional to the cube of its radius, multiplied by a constant factor of 43π.

6. Area of Parallelogram = base x height

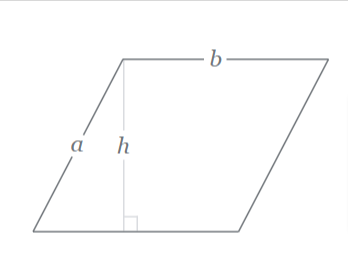
This is the most common and straightforward method. Imagine a parallelogram with a base of length “b” and a corresponding height “h” (perpendicular to the base). The area (A) can be calculated using this formula.

7. Pythagorean Theorem: a² + b² = c²

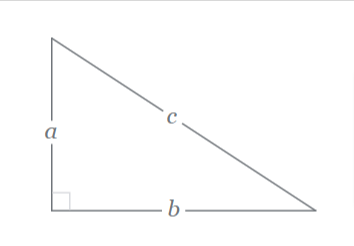
The Pythagorean Theorem is a fundamental concept in geometry that relates the lengths of the sides in a right triangle. In a right triangle (a triangle with one 90-degree angle), the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides (called legs).

8. Slope Formula

The slope formula is a mathematical tool used to calculate the steepness and direction of a non-vertical line. It tells you how much the line slants up or down as you move from left to right. Here’s the breakdown:

m = (y₂ – y₁) / (x₂ – x₁)

Where:

• m represents the slope of the line.
• (y₂, x₂) and (y₁, x₁) are the coordinates of two different points on the line.
• (y₂ – y₁) represents the change in the y-coordinate (rise).
• (x₂ – x₁) represents the change in the x-coordinate (run).

9. Distance Formula

The distance formula, also known as the Euclidean distance formula, is a mathematical equation used to calculate the straight-line distance between two points in a coordinate system.

Here’s how it works:

1. In two dimensions (2D):

Imagine you have two points, named A(x₁₁, y₁) and B(x₂, y₂), on a graph with x and y axes. The distance between these two points, represented by the letter “d”, can be found using the following formula:

d = √[(x₂ – x₁)² + (y₂ – y₁)²]

Where:

• √ represents the square root.
• (x₂ – x₁)² represents the difference in x-coordinates squared.
• (y₂ – y₁)² represents the difference in y-coordinates squared.

2. In three dimensions (3D):

If you’re working in 3D space, imagine points A(x₁₁, y₁₁, z₁) and B(x₂, y₂, z₂). The distance formula becomes:

d = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²]

Where the additional term (z₂ – z₁)² accounts for the difference in z-coordinates squared.

10. Midpoint Formula

The midpoint formula is a mathematical tool used in coordinate geometry to find the exact coordinates of the midpoint of a line segment.

Here’s how it works:

Imagine you have two points on a graph, identified by their coordinates:

Point 1: (x₁, y₁)

Point 2: (x₂, y₂)

The midpoint of the line segment connecting these two points will have the following coordinates:

Midpoint = ((x₁ + x₂)/2, (y₁ + y₂)/2)

This formula essentially takes the average of the x-coordinates and the average of the y-coordinates of the two endpoints. This is because the midpoint lies exactly between the two points in both the horizontal and vertical directions.

11. Equation of a line

The equation of a line formula describes the mathematical relationship between the x and y coordinates of any point that lies on that line. There are several different ways to express this formula, depending on what information you have about the line. Here are the three most common forms:

1.  Slope-intercept form:

This is the most widely used form, written as

y = mx + b

Where:

• m is the slope of the line, which represents its steepness and direction. A positive slope means the line goes up as you move to the right; a negative slope means it goes down; and a slope of 0 means it’s a horizontal line.
• b is the y-intercept, which is the point where the line crosses the y-axis.
• x and y are the coordinates of any point on the line.

2. Point-slope form:

This form is useful if you know the slope (m) and the coordinates of one point (x1, y1) on the line:

y – y1 = m(x – x1)

3. Standard form:

This form expresses the equation in terms of all three variables, although it’s not always the most convenient.

Ax + By + C = 0

Where:

A, B, and C are constants.

Why is memorizing ACT Math formulas important? The ACT has a time crunch. There are 60 questions, which you have to answer in 60 minutes. This means you’ve got just one minute per question. That’s why knowing the key formulas is crucial. They’ll save you precious time and mental energy, allowing you to focus on strategically solving problems instead of scrambling to remember obscure equations.

12. Quadratic Formula

The quadratic formula is a mathematical equation used to solve quadratic equations, which are equations of the form:

ax² + bx + c = 0

Where:

• a, b, and c are real numbers, and a ≠ 0.
• x is the unknown variable.

13. Factoring: Know how to factor common factors, perfect squares, and differences of squares.

Factoring is the process of breaking down a polynomial expression into its constituent parts, like breaking down a number into its prime factors. It’s a crucial skill in algebra as it simplifies expressions, helps solve equations, and forms the foundation for many other concepts.

14. Logarithms: logₐ(b) = x means aˣ = b (be familiar with common log bases like 2 and 10)

The statement logₐ(b) = x is equivalent to the equation aˣ = b, and understanding this relationship is key to grasping logarithms. Let’s break it down:

Imagine a tiny magnifying glass.

• The base (a): This is like the magnifying glass itself. It determines how much things get magnified (or shrunk) when you look through it. Common bases include 2 (for binary logarithms) and 10 (for common logarithms).

• The argument (b): This is like the object you’re looking at through the magnifying glass. It’s the number you’re trying to understand in terms of the base.

• The exponent (x): This is like how many times you turn the magnifying knob. It tells you how much you’ve magnified (or shrunk) the object using the base.

The equation logₐ(b) = x means:

• You started with the number b (the object).
• You used the base a (the magnifying glass) and its power x (the number of turns) to transform it.
• This transformation resulted in the number aˣ (the magnified/shrunk object).

In simpler terms:

• logₐ(b) asks, “To what power must I raise a to get b?”
• aˣ = b says, “Raising a to the power x gives you b.”

15. Linear Function

In simpler terms, a linear function is any function whose graph forms a straight line. Mathematically, a linear function can be expressed in two main forms:

1. Slope-intercept form:

y = mx + b

Where:

• y is the output (dependent variable).
• x is the input (independent variable).
• m is the slope, which determines the steepness and direction of the line.
• b is the y-intercept, which is the point where the line crosses the y-axis.

2. General form:

ax + by = c,

Where:

• a, b, and c are constants.

16. Quadratic Function

The quadratic formula is a mathematical equation used to find the roots (also known as zeros) of a quadratic function. These roots represent the x-values where the function equals zero.

f(x) = ax² + bx + c

Where:

• a, b, and c are real numbers, and a ≠ 0 (otherwise it wouldn’t be a quadratic function).
• x is the variable.

17. Absolute Value Function

The absolute value function, denoted by |x|, represents the non-negative version of a number. In simpler terms, it expresses the distance of a number from zero on the number line. Here’s the formula for the absolute value function:

|x| = {

x, if x ≥ 0

-x, if x < 0

}

This means,

• If the number (x) is already non-negative (greater than or equal to zero), then its absolute value is simply itself (x).
• If the number (x) is negative, then its absolute value is the negative of itself (-x).

18. Standard Deviation

There are two main formulas for standard deviation, depending on whether you’re dealing with a population (the entire dataset) or a sample (a subset of the data):

1. Population Standard Deviation

This formula applies when you have data for the entire population you’re interested in. It’s denoted by the symbol σ (sigma).

σ = √( Σ(xᵢ – μ)² / N )

Where:

• μ (mu) is the population mean (average).
• xᵢ is each individual value in the dataset.
• N is the total number of values in the population.
• Σ (capital sigma) means “sum of” across all values.

2. Sample Standard Deviation

This formula is used when you only have data for a sample of the population and want to estimate the population standard deviation. It’s denoted by the symbol s.

s = √( Σ(xᵢ – x̅)² / (n – 1)

Where:

• x̅ (x bar) is the sample mean (average).
• xᵢ is each individual value in the sample.
• n is the number of values in the sample.

19. Trigonometric Ratios

Trigonometry is all about relationships between sides and angles in right-angled triangles. Trigonometric ratios help us quantify these relationships, and there are six main ones to remember:

SOH CAH TOA: This mnemonic is a handy way to recall the formulas for the primary ratios:

• Sine (sin): Opposite side over Hypotenuse (SOH)
• Cosine (cos): Adjacent side over Hypotenuse (CAH)
• Tangent (tan): Opposite side over Adjacent side (TOA)

The reciprocals of sine, cosine, and tangent also have names and uses:

• Cosecant (csc): Hypotenuse over Opposite side (1/sin)
• Secant (sec): Hypotenuse over Adjacent side (1/cos)
• Cotangent (cot): Adjacent side over Opposite side (1/tan)

20. Pythagorean identity

This formula, sin2(θ) + cos2(θ) = 1, is known as the Pythagorean identity in trigonometry and holds true for any angle θ. It represents a fundamental relationship between the sine and cosine functions defined on the unit circle.

Read Also: 5 Best ACT Tips and Tricks to Achieve Your Desired Score

From the Desk of Yocket

The ACT math formulas are essential tools for success on the test. Knowing and understanding them allows you to approach a variety of problems with confidence and efficiency. Without a grasp of these formulas, you might struggle to solve problems even if you have a strong conceptual understanding of math.

While formulas are important, simply memorizing them isn’t enough. It’s important to remember that understanding the underlying concepts behind the formulas is even more important. Simply plugging numbers into formulas without genuine comprehension can lead to errors and missed opportunities. You should understand when, how, and where to apply them. The ACT exam often tests your ability to choose the right formula for a given situation, not just recall it from memory. 

---

Frequently Asked Questions

Can I use a calculator for the ACT Math test?

Yes, you can use an approved scientific calculator on the ACT. Graphing calculators and calculators with other features are not allowed.

What are the main topics covered in the ACT Math test?

These are some of the topics covered in the ACT Math:

• Pre-algebra (basic operations, fractions, decimals, percents)
• Algebra (expressions, equations, inequalities, functions)
• Geometry (lines, angles, shapes, area, volume)
• Trigonometry (basic concepts, ratios)
• Probability/statistics (data analysis, chance, probability)

How can I prepare for the ACT Math test?

There are many resources available to help you prepare for the ACT Math test, including ACT Math practice tests, study guides, and online courses. The official ACT website also has a variety of free resources.